Complete Analysis and Design of Two-way Slab System Moment Coefficient Method

Analysis and Design of Two-way Slab System 

(Two-Way Slabs Supported on Stiff Beams or Walls)

Moment Coefficient Method

Bangladesh National Building Code (BNBC-2020)

6.5.8.2 Scope and limitations:  

6.5.8.2.1 The provisions of this section may be used as alternative to those of Sections 6.5.1 to 6.5.7 for two-way slabs supported on all four edges by walls, steel beams or monolithic concrete beams having a total depth not less than 3 times the slab thickness.

6.5.8.2.2 Panels shall be rectangular with a longer to shorter center to center support span ratio of not greater than 2.

6.5.8.2.3 The value of  shall be greater than or equal to 1.

Steps in Moment Coefficient Method

 

Step 01: panel/slab case determination from cases (From Code, given at the end)

Step 02: Determination of thickness of the slab panel,

               h_min = perimeter/ 180 = 2(l_a + l_b)/180

Step 03: Calculation of factored loads on slab

Step 04: Calculation of m = l_a/ l_b

Step 05: Determination of moment coefficients from tables.

Step 06: Calculation of moments and then design.

Step 07: Apply reinforcement requirements.

Step 07: Shear check.

Calculation of moments

Example:

·       Live Load = 45 psf 

·       fc′= 3 ksi

·       fy = 60 ksi

·       super dead load = 0.02 ksf

Step 01: panel/slab case determination from cases  

Two adjacent edges discontinuous, hence case = 4

Step 02: Determination of thickness of the slab panel

h_min = perimeter/ 180 = 2(la + l_b)/180 = 2(18+20)/180 = 0.422*12  5.5 inch

Step 03: Calculation of factored loads on slab

Total dead load = 5.5/12*0.150 +0.02=0.089 ksf

Live load = 45 psf = 0.045 ksf

Factored dead load, w_{u dl} = 1.2*0.089=0.11 ksf

Factored live load, w_{u ll} = 1.6*0.045=0.072 ksf

Total factored load, w_u =0.11+0.072=0.182 ksf

Step 04: Calculation of m = la/ l_b

m = la/ l_b = 18/20=0.9

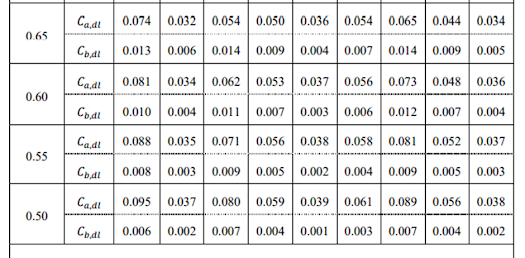
Step 05: Determination of moment coefficients from tables (Provided at the end)

C_a,neg = 0.060 (BNBC-Table 6.6.8)

C_b,neg = 0.040 (BNBC-Table 6.6.8)

C_a,pos,dl =0.033 (BNBC-Table 6.6.9)

C_b,pos,dl = 0.022 (BNBC-Table 6.6.9)

C_a,pos,ll = 0.039 (BNBC-Table 6.6.10)

C_b,pos,ll = 0.026 (BNBC-Table 6.6.10)

Step 06: Calculation of moments and then design

Ma,neg =	Ca,neg * Wu * la2	0.060*0.182*182	= 3.54	3.54
Mb,neg =	Cb,neg * Wu * lb2	0.040*0.182 *202	= 2.91	2.91
Ma,pos =	Ca, pos, dl * Wu, dl * la2	0.033*0.11*182	= 1.18	1.70
	Ca, pos, ll * Wu, ll * la2	0.022*0.072*182	= 0.51
Mb,pos =	Cb, pos, dl * Wu, dl * lb2	0.039*0.11*202	= 1.72	2.46
	Cb, pos, ll * Wu, ll * lb2	0.026*0.072*202	= 0.74

Step 07: Apply reinforcement requirements

Consider 12 inch width of strip, b=12 inch

d_avg = 5.5 - 0.75- 0.375 (#3) = 4.375

	Ma,neg	Mb,neg	Ma,pos	Mb,pos
	3.54	2.91	1.70	2.46
	0.072	0.058	0.034	0.049
As , in2	0.20	0.15	0.089	0.13
As , in2 , min (0.0018*b*h)	0.12	0.12	0.12	0.12
Spacing, S ≤2h &18’’	(Area of used bar*12)/Total Area of Bars (as × 12)/(As) = 6’’ c/c < 2*5.5=11 &18’’	8’’ c/c	11’’ c/c	10’’ c/c

Step 07: Shear check

W_a = 0.60 (BNBC-Table 6.6.11)

W_b = 0.40 (BNBC-Table 6.6.11)

W _{La (Ult)}  = 0.60*0.182 = 0.11 kip/ft

W _{Lb (Ult)}  = 0.40*0.182 = 0.07 kip/ft

v_uLa = 0.11*[(18/2)-(4.375/12)] = 0.95      [v_uLa =W _{La (Ult)}  *( L_a/2 – d)]

v_uLb = 0.07*[(20/2)-(4.375/12)] = 0.67      [v_uLb =W _Lb(Ult)  *( L_b/2 – d)]

ØV_c =  0.75(2  bd) = 0.75*2*1* *1*(4.375/12)=0.95

V_u = maximum of v_uLa  and  v_uLb

Hence,  ØV_c ≥ V_u , ok.

BNBC- Tables